Scaling in LP problems is about the range of magnitude of values that appear in the equations. GRTMPS has some overall Model Scaling factors that can be used to improve the range of magnitude of coefficients in the matrix.
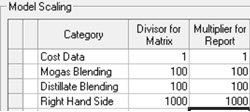 |
These are the default values filled in the Model Scaling grid on the main Model note. These values are also used if there is no entry. (If you have table format input data, scaling factors will be in TABLE 990.0). Factors are normally given as powers of 10 so that applying them moves the decimal point. |
Values are divided by the Divisor as they go into the equations, and the related results are multiplied by their Multiplier when retrieved from the solution. Property scaling is normally symmetrical - set to the same value in both directions - so that the impact is in the matrix equations without affecting how qualities are input or reported. In a purely linear model you can set different values for gasoline and distillate blending but in recursed models all blending is scaled using the Mogas one.
The default scaling for properties is 100. The goal was to make values closer to 1. So, for example, an octane of 98 becomes 0.98, and percentages, such as volume distilled at 70degC, would look like fractions. it wouldn’t be very helpful if a density value of 0.75 kg/m3 became .0075, so the internal blend basis properties, .WT and .VL, that are calculated from DEN are not scaled. Most older GRTMPS models had a pseudo-density property, e.g. DNX, defined as DEN times 100 or 1000. The pseudo-property was needed because DEN was reserved for weight/volume conversions and couldn’t be used for specifications. The multiplier was to undo the impact of the property scaling. So DEN=0.75 became DNX=75, and then the default scaling took it back to 0.75 (In a weight balanced model, of course, DNX as a volume blending property would be divided by DEN, so in fact the co-efficient would come out as the multiplier, 100, and then be scaled to 1).
The effect of scaling is easily seen in the matrix. For example, the weight based demo model has two modes on the reformer, high and low severity, that produce 98 and 103 octane reformate. These are blended together into a gasoline component pool (if you do Exercise 16). Each component brings in its octane value on a component-to-blend vector, and the estimated pool octane appears as a negative value on the (pool)WT vector. It’s a volume property in a weight model so they have been divided by density
With the property scaling set to 1, as the model is distributed, the equation is
Row = RRAARE#5#R00_)Q Type = FIX RHS = 0.000000
RRAARE#5#R00_)D = -1 RRAARE#5#R98_~ = 125.59272075
RRAARE#5#R10_~ = 128.66958151 RRAARE#5#WT = -128.66958151
With the default scaling, which is 100, the values would all become smaller.
Row = RRAARE#5#R00_)Q Type = FIX RHS = 0.000000
RRAARE#5#R00_)D = -0.01 RRAARE#5#R98_~ = 1.25592721
RRAARE#5#R10_~ = 1.28669582 RRAARE#5#WT = -1.28669582
| The 25 worst scaled rows | (1) | The 19 worst scaled rows | (100) | |
| Row Name | Scaling Factor | Row Name | Scaling Factor | |
| RRAAHG#6#V40_)Q | 1146186 | RRAA#HG#6BAL | 1142857 | |
| RRAA#HG#6BAL | 1142857 | RRAAHG#6#FLH_)Q | 1142857 | |
| RRAAHG#6#DEN_)Q | 1142857 | RRAAHG#6#E35_)Q | 1142857 | |
| RRAAHG#6#FLH_)Q | 1142857 | RRAAHG#6#E36_)Q | 1142857 | |
| RRAAHG#6#CLD_)Q | 1142857 | RRAAFUEUT | 941176 | |
| RRAAHG#6#POR_)Q | 1142857 | RRAALSF_~VAN_)L | 644547 | |
| RRAAHG#6#CET_)Q | 1142857 | RRAADSL_~SPM_)L | 147586 | |
| RRAAHG#6#E36_)Q | 1142857 | RRAABIO_~SPM_)L | 147586 | |
| RRAAFUEUTB | 1000253 | RRAAHTO_~SPM_)L | 147586 | |
| RRAAHSH_~BAL | 941176 | RRAAVG#6#SPM_)Q | 147586 | |
| RRAALSF_~VAN_)L | 644547 | RRAAVG#6#VAN_)Q | 54361 | |
| RRAAKE#6#VAN_)Q | 445292 | RRAAAR#6#SPM_)Q | 32665 | |
| RRAADSL_~SPM_)L | 147586 | RRAADO#6#SPM_)Q | 24500 | |
| RRAABIO_~SPM_)L | 147586 | RRAADSL_~CTA_)R | 18920 | |
| RRAAHTO_~SPM_)L | 147586 | RRAADO#6#SUL_)Q | 15956 | |
| RRAAHY#6#SPM_)Q | 147586 | RRAAJET_~SPM_)L | 15000 | |
| RRAAVG#6#SPM_)Q | 120000 | RRAAHYD_~BAL | 10840 | |
| RRAAVG#6#VAN_)Q | 54361 | |||
| RRAAAR#6#SPM_)Q | 32665 | |||
| RRAADO#6#SPM_)Q | 24500 | |||
| RRAADSL_~CTA_)R | 18920 | |||
| RRAADO#6#SUL_)Q | 15956 | |||
| RRAAJET_~SPM_)L | 15000 | |||
| RRAAHYD_~BAL | 10840 |
If the in-row scaling is not affected by moving the decimal point, how is it that some rows have dropped out of the list? Lets have a look at what's changed.
The vanadium balance row for the kerosene pool, RRAAKE#6#VAN_)Q, in the unscaled matrix is:
Row = RRAAKE#6#VAN_)Q Type = FIX RHS = 0.000000
RRAANP#5#VAN_)D = 0.5 RRAAKE#6#VAN_)D = -1
RRAAKE#6#KEBRT = 2.2457175e-006
In the scaled matrix it is:
Row = RRAAKE#6#VAN_)Q Type = FIX RHS = 0.000000
RRAANP#5#VAN_)D = 0.005 RRAAKE#6#VAN_)D = -0.01
The row scale has improved because the very small value contributed by the Kero cut from crude BRT has disappeared. Reduced by two magnitudes smaller it is below the 5E-07 threshold for inclusion the matrix. Its probably a good thing that this value has disappeared. Vanadium is being measured in ppm, so that number represented 2 parts per trillion and is almost certainly just some noise from the calculations for filling in the crude library – and even if it is accurate it is still effectively nothing for practical purposes.
However, sometimes removing small values is not a good thing. If the relationship is real, and there could be a large activity on the vector, then it would have a meaningful impact on the row balance and should be there. This is the situation we have with the various quality balance rows for HG# - the hydrotreated gas oil – that have dropped out of the bad scaling list. This pool is the output from the gasoil hydrotreater. It’s properties are primarily being set equal to those of the feed pool, HY#, via Adherent Recursion linked to a simple non-linear process model.
Unscaled Cloud balance:
Row = RRAAHG#6#CLD_)Q Type = FIX RHS = 0.000000
RRAAHYD10G_^ = -9.745695 RRAAHY#6#SPM_)D = 8.7500000e-006
RRAAHY#6#CLD_)D = 0.9745695 RRAAHG#6#CLD_)D = -1 RRAAHG#6#WT = 10
The base cloud index value comes in on the unit vector (HYD10G) and there are links to the error vector for the feed pool cloud in case it is changing, and also to the feed sulphur, SPM. Feed sulphur does not have a direct effect on the cloud, but it does alter the yield. Since all qualities in distributed-recursion models are carried by a quantity of material there is an assumed yield fraction used in the calculation of the base cloud value, to scale from feed tons to gasoil tons. Since delta-sulphur leads to delta-yield that means also delta-cloud.
Divided by 100 though, and the sulphur factor goes below the threshold and drops out.
Scaled Cloud Balance:
Row = RRAAHG#6#CLD_)Q Type = FIX RHS = 0.000000
RRAAHYD10G_^ = -0.09745695 RRAAHY#6#CLD_)D = 0.009745695
RRAAHG#6#CLD_)D = -0.01 RRAAHG#6#WT = 0.1
Without it, the match between the input cloud and the output cloud in the preliminary solutions on the non-converged passes won't be as good so the economic drivers might not be right. The linear approximation will not be as good at predicting what the simulator that is doing the unit calculations is going to say so it could be harder to achieve a converged solution. So for this situation, I like the unscaled equations better.
Removing the scaling also looks like a good idea when using DEN directly for specifications etc, since without the multiplier on the pseudo-property, these values will be closer to 1 without it. But we shouldn't just rely on our reasoning. SLP optimization often surprises, so to confirm my understandig, some years ago now, I made the comparison for several larger models. I found that no property scaling was better, on balance, so I always set it to 1. 100 was a good value for a long time, but with the additional precision of modern computers and increasing detail in process modelling, means it is often no longer the best option.
If you are still using the default value, you should try changing to 1. Make sure you check several cases and multi-starts before deciding which is better for your models. These kinds of changes in the matrix are just the sort of thing to highlight the chaotic nature of SLP, so the comparison is going to be a bit messy. You need to see how it influences the probability of finding a good solution, instead of just doing a simple before/after comparison of your current base run.
Badly scaled rows are still something to be avoided, but there are often more targeted options for reducing the range. Very small property values, like the vanadium, could be filtered out when the crude library is generated. The sulphur factors in the hydrotreater model would all be a more reasonable size if the calculation was driven from sulphur %wt instead of ppm, solving the scaling problem without losing any information.
Will we ever get around to changing the default? Maybe in g6. Until then, you will have to set it yourself.
19th August 2020.
You may also use this form to ask to be added to the distribution list so that you receive an e-mail when new articles are posted.