Although LP in the refinery business usually means a production planning model with detailed representations of the process units and blending, it is also possible to apply optimization methods to other business activities, such as product distribution. That is, when there are multiple possible sources of products, how do we best supply each of our customers, taking into account the costs and limitations of storage and transportation facilities. Note that I am NOT talking about routing the deliveries on the day as that sort of logistics problem needs specialist algorithms and isn't usually amenable to LP optimization. These models are often used to work out best contract options for facilities – such as how many trains to lease - and for balancing your own production and demand against options for buying and selling on the open market. Such models are usually characterized by having many, many locations, but few streams
For example, this is part of the Distribution demo model – (using a multi-location extension to the Block Diagram tool that is in the new H/PLANET interface for GRTMPS.)
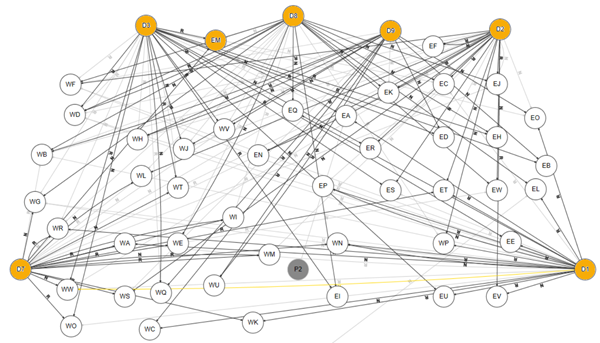
Product supplies are normally modelled as purchases from your own production facilities, plus any third-parties that you might be able to get supplies from – in this model the locations D1 through D9 (marked in orange) are the source locations. The requirements for products– by regions, districts or even by individual customer or contract, depending on the granularity you can manage - are modelled as sales, often fixed quantities based on expected or existing contractual obligations. The model will contain transportation options to move material from purchase locations to sales sites. These might be real physical movements to actual locations, perhaps via intermediate points such as ports or terminals. They might be virtual movements to imaginary locations. These pretend sites are a useful way of giving something a different price. When you have a lot of separate sales of the same material, doing them at different locations is easier than setting up lots of cost accounts or stream aliases at one location.
 |
That can make for a very long list of location codes. Combining upper and lower-case letters with the digits 0-9 will give you several thousand two-character identifiers. If you need more, you have to start using non-alphanumerics and can end up with some odd codes, that are not so easy to type in, or say out loud. (Copy/Paste from Word is one method; or use the number keypad and the ASCII codes). |
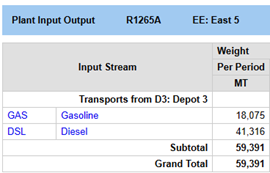
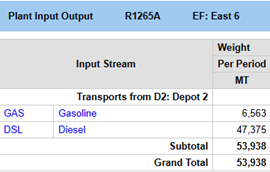
The job of the distribution model is to decide where the material for each sale will come from. It isn’t always the cheapest source or the shortest supply route for each one, considered in isolation, as there is competition with other deliveries. The point of doing the optimization is to get the best balance over the whole network. The solution to this distribution case indicates that
| customer East 5 should be supplied from Depot 3 | and customer East 6 should be supplied from Depot 2. | |
 |
 |
| However, the proposal that Diesel will be shipped to East 1 from Depot 1 but Gasoline from Depot 2 would make for more complex logistics contracts, and is not acceptable | 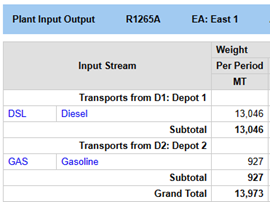 |
It is, in fact, a common requirement of distribution problems that each customer should be supplied from one single source. East 1 must receive both Diesel and Gasoline from Depot 1 or Depot 2.
“Or” constraints require MIP. Having only one of a number of options active at a time is the territory of SOS – Special Order Sets – Type 1. If you are supplying just one product with a single transport option from each supplier, then you could make an SOS on those transportation options. With two or more products each option corresponds to at least two variables. We can still use a set, though, if we collect the information from the movements together so that activity on a supplier-customer combination is reflected in a single variable, no matter how many products or transport routes are involved.
Transferring information about transports to a dummy process unit will do the trick. The process unit will have to exist at the each of the customer locations – but at least we can use the same one everywhere.

We will need one limit per supplier to drive the counts. The same names can be used for every receiving location. (The row and column names in the matrix will be distinct because they include the location code). I define the operating parameters and assign them to the “Deliveries From” process unit.
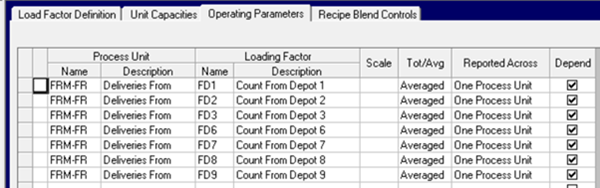
Scaling factor is left blank since these are all going to be fixed to zero so there is nothing interesting to report. Ticking the Depend column means that I can set the limits using ** as a location code. Equivalent in a TABLE based model to using $FIX in TABLE 2FR.0 (or in H/PLANET to classifying it as a Driver Row). Using ** for the location code on the limits is really useful as otherwise I would need hundreds of records to enter them for each customer location individually.
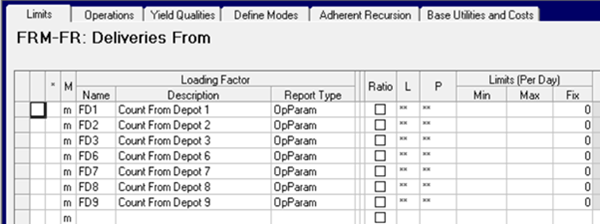
Connect the transport options to the Loading Factor for the source Depot.
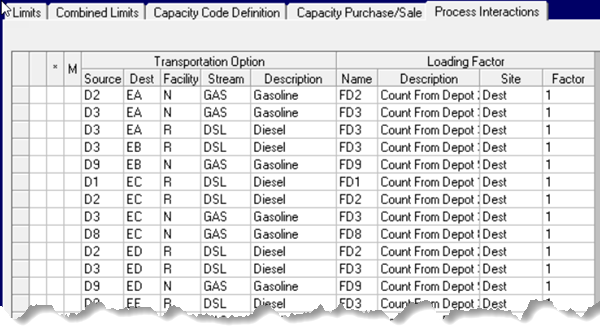
The connection is made at the destination location, because that is where we need the vectors for the SOS.
Then we go to the process unit and connect the operations to the driver rows.
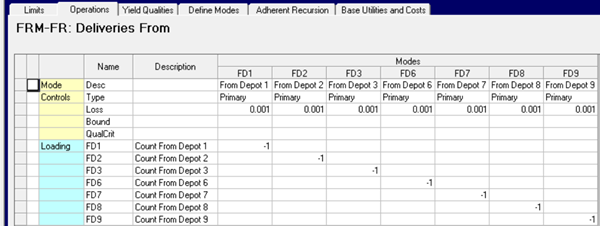
Having used a positive loading on the transportation, a negative is used here so that the quantities balance.
We are creating a very large number of equations like:
Row = EPAAFD1_]PE Type = FIX RHS = 0.000000
EPAAFRMFD1_^ = -1 0AAND1EPGAS_~ = 1
0AARD1EPDSL_~ = 1
That is, the process operation activity must be equal to the sum of the movements of gasoline and diesel from D1 (Depot 1) to the customer location identified as EP. Even though this is a MIP problem, we don’t need to use binary vectors. The SOS doesn’t depend on the amount of activity on the vector, only whether there is any. The next step is to add the sets.
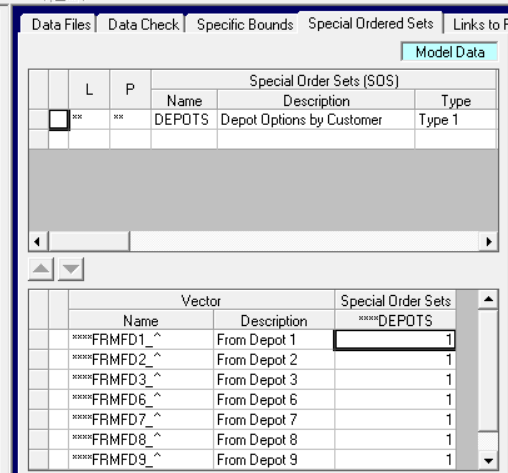 |
Here we again use the wild card “**” for the Location (L) so that one SOS is generated for each location, having the Vectors for that location as its members. And also ** for the period, so it is built for each in the case, whatever they are called. The rest of the vector name needs to match exactly what is in the matrix. Process unit modes are built with (UNT)(MOD)_^. There are some locations in the model that don’t have these modes because the unit doesn’t exist there. No SOS will be written for them because they must have at least two members. Check the MTX file to confirm that you have been successful. You should see sometthing like: |
If you are using an optimizer that doesn’t support SOS, you can use an if…then structure to drive a binary vector to indicate the on/off status of each supplier. An additional limit is set per customer to control the sum of those to one. Or maybe some other value, as this method offers more flexibility. Perhaps 2 depots would be considered acceptable for a particularly large consumer.
When you optimize now, you should find that every Customer is supplied by only one Depot.
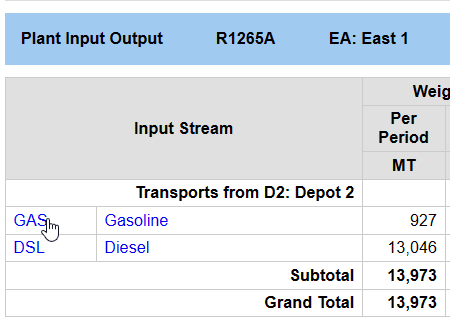
| It is not uncommon to take a couple of rounds of adjustment to turn up an optimal solution to these large problems – particularly where supply and demand data are coming from different departments are not necessarily initially in balance. When I started adjusting the distribution model for this case, I had some INFE solutions. This means that the relaxed problem, without the SOS, is infeasible. As you can’t make a linear problem feasible by adding more constraints, there is no point in imposing the SOS until the base problem is feasible. So when you are setting up a new case, turn the SOS off. If you are using the Table based input, then this is easily done by deactivating TABLE 197.0 in some way. In the database the SOS is part of the model structure and is not easy to turn off on a case-by-case basis. However, you can make it irrelevant by commenting out the driver rows. Once you have an OPTM solution, turn the SOS back on |  |
If your problem solves to MINF, it is MIP infeasible. The relaxation is optimal, but there is no solution once the SOS condition is imposed. For example:

If you look at the solution print in the listing file, the vectors that are breaking the rules will be marked as infeasible. Searching for ** finds the first one. EA is breaking the only one supplier rule by having shipments from both D1 and D3
Number Column At Value Input Cost Reduced Cost
C 116 EAAAFRMFD1_^ BS 9.053 0 0
C 117 EAAAFRMFD2_^ BS 0 0 0
C 118 EAAAFRMFD3_^ ** 4.92 0 0
C 119 EAAAFRMFD6_^ BS 0 0 0
Now we have to go back and check if all the routes are there – is there at least one of the Depots can supply both products. Or maybe the problem is insufficient product at any one of the Depots or a lack of capacity on the transportation routes. Eliminating that problem, I try again and again, until I have an OPTM solution. As this is the demo model, I get to just adjust the numbers until everything works. In real life, you might have to go back to your colleagues and ask them to adjust the requirements or find additional supplies in order to balance out the network. That is, the infeasibilities themselves can provide useful information about your situation.
It is, of course, also possible to combine distribution and refinery planning, by adding this kind of network representation onto your refinery model - if you think there will be benefits that make it worth the extra complexity.
From Kathy's Desk, 12th March 2024.
Comments and suggestions gratefully received via the usual e-mail addresses or here.
You may also use this form to ask to be added to the distribution list so that you are notified via e-mail when new articles are posted.