If you constrained an operating parameter to take a specific value, forcing it away from the optimal point, you would expect to see an incentive on the limit. But one of our users noticed that it was always coming out blank for certain parameters – and then he figured out why with the help of the matrix comparison tool. I’ve replicated the issue in the weight demo model, so we can all see what’s going on and how a simple adjustment restored the reporting of an incentive.
If you start off with a wide enough min-max range for an operating parameter (or any other constraint), such that the optimal value is not limited, the solution will balance on the perfect point where there is exactly no incentive to do anything else, because you would lose money. And the results would be like so:
Then, in order to see how sensitive the objective value is to severity, set up a case generator file to fix it to a sequence of values from the min to the max.
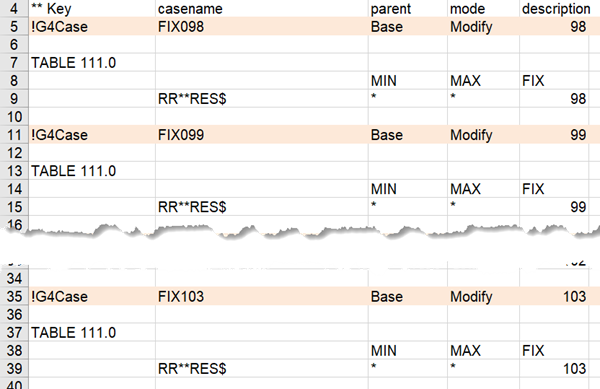
The objective function value changes as expected, peaking at 102
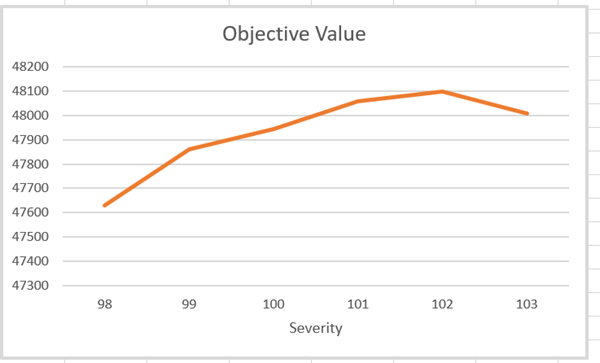
- but in every single one of the reports, the incentive is blank.

Its not simply a reporting problem, because the solution print also shows a zero value.
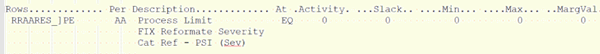
My first reply when asked about this problem was that it was probably some issue with degeneracy or chaos – but it turned out to be much simpler. My questioner thought to compare the matrix from one of the fixed cases to the open case, and this revealed more changes than expected
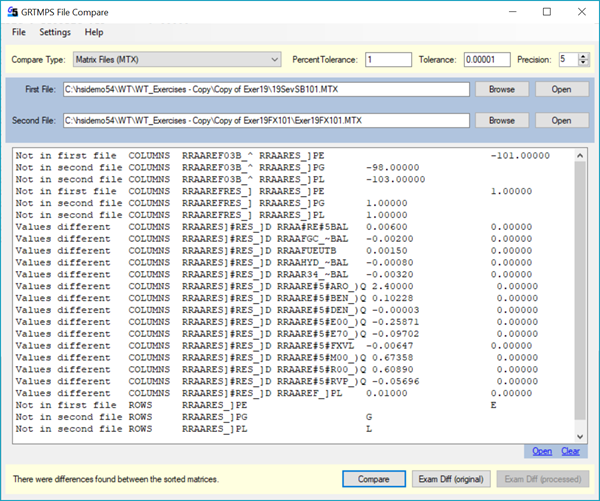
RES_]P changing from the two G and L rows, to one E row, is expected. The surprise is that all the RES_]D values have gone to zero. That vector is the delta for severity impact on process unit outputs. Then I realised something useful. This parameter is being used as an input to a non-linear process unit representation in a PSI workbook. When an Adherent Recursion input is fixed and cannot be optimized, the matrix generator code treats it as a simple constant – passing the value into the non-linear calculations, but not bothering to calculate any shift values, since the parameter can’t change. This saves time and reduces the scope for unhelpful results on infeasible passes. But it also means that if the constraint were relaxed in that matrix, nothing would happen. So no incentive. Mystery solved.
To retain the structure and generate an incentive value, use min and max constraints instead, with a narrow gap.

Now there are incentives
as well as objective functions.
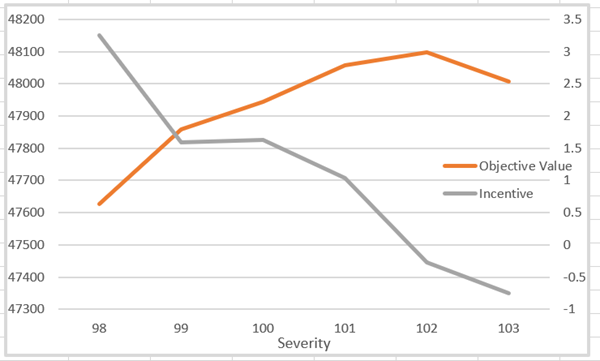
When positive, it is the max which is constraining, when negative, it is the minimum. You can see how it switches over around the optimal point. A little wiggle room can also be helpful in maintaining feasibility and avoiding local optima.
Thanks, Rowell.
P.S. If you want to replicate this yourself, use the Weight demo model, Exercise 19, but switch from calculating severity from reformate RON, to predicting RON from severity.
From Kathy's Desk, 19th July 2018.
Comments and suggestions gratefully received via the usual e-mail addresses or here.
You may also use this form to ask to be added to the distribution list so that you are notified via e-mail when new articles are posted.