58) Crude Marginal Value in Multi-Refinery Models

“I have a multi-refinery model and it reports the crude marginal values at each site.  Where can I find the over-all marginal value for a crude?”

Each stream has a marginal value at every location where it exists.   This is because there is a balance row which adds and subtracts all the sources and consumptions of each stream at that location. There is no over-all marginal value reported for streams that exist at both locations because there is no equation which combines the balances at both sites. (If there was crude could be bought at one and used at the other as there would be no way of telling them apart.) But maybe we can work something out from the individual marginal values.  I used our Corporate Demo model to have a look.

In the absence of any constraints on the purchases, the optimal solution will be balanced at each location at the point where the marginal value is equal to the price.

When the price is the same for both sites and there are no limits, the overall marginal value is also the price. The 47,000th or so bbl of Arab Light for the day at refinery 33 is worth the same as the 42,000^th-ish barrel at refinery 11.

What if the price is different? You might pay the same base cost per barrel, but delivery costs could be different. If transportation adds $0.25/bbl at Refinery 33 but 0.50$/bbl at Refiner 11 then

Each will still balance where the price equals the value. (Note that the change was not enough to alter the amounts taken – the other two crudes available in these models are both more expensive). With different prices comes different marginal values at the individual sites.

Now what is the marginal value overall? Consider that the marginal value on a stream balance row can be understood to be, roughly, an indication of the additional revenue that you would earn if you had another barrel for free, to do what you want with.  (See Note #37)  If you had such a barrel and could use it any site you chose, then to maximize profit you should process it at the location that has the best marginal value, which is the one where it costs the most.  The overall marginal value is equal to the maximum of the marginal values at the sites. In the absence of a constraining limit on the amounts purchased, this is the maximum price.

What happens, though if there is some limit on the amount of this crude that can be delivered this month?   The optimal solution is using more than 89,000 bbl/day. What if there are only 85,000 bbl/day available?   This is exactly the kind of question that pushes us to run a multi-site model, to find the best allocation of a limited resource.

It is easy enough to add a limit to the total purchases across the two sites. This gives

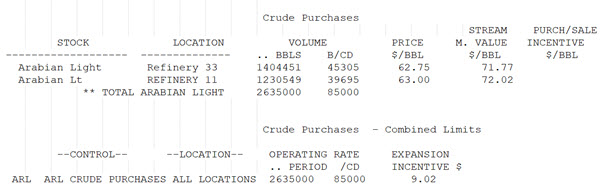
The amount of crude allocated to each site is reduced. You might have expected it to continue to take the previously identified optimal amount at the site with the best value, and replaced it with the next best option at the other – but there are limited alternatives in this case, and they are expensive – so there is still an incentive to take as little of the other crudes as possible.

The marginal value is now more than the price to show that the solution has been prevented from reaching the optimal Arab Light amount at either site.  There is no incentive on the purchases, though, because of the overall limit. If you bought more at one site it would be balanced out by a reduction at the other. In the absence of individual limits, the solution is balanced at the point where switching is neutral – if money would be made or lost by reallocating it would have done so.

There is an incentive on the overall limit. If you could buy another barrel it would add $9.02 to your profits – the difference between the cost and the stream value (at both sites). This is different from the stream marginal value because you would have to pay for it, whereas if the stream balance row is relaxed, you get that additional barrel for free so you don’t have to deduct the purchase price. The MV at each site is equal to the price plus the overall limit incentive.  

Back to our original question – what is the overall marginal value? Again ask the question – if you had a barrel for free to do what you want, where would it go? To the site with the best value. So the overall marginal value is still equal to the maximum value at any individual site, because that is where you would put it. Having an overall limit on the purchase affects the values, but not their meaning.  If I add a purchase at zero price for 1 more bbl in total it should go to Refinery 11

And it does….

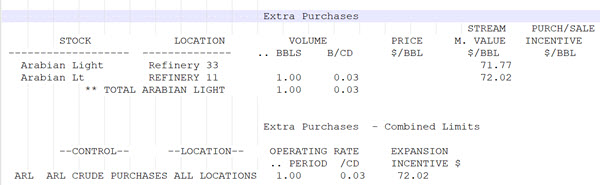
So the marginal value for a crude over a multi-refinery model is the maximum marginal value that it has at any site.

Note that these are simple models with only a few crudes and a single processing train. If you try adding a one more bit of a crude for free to a real model the forces of chaos might strike and your solution might not come out so neatly.

Thanks to Alessandro Martini for the interesting question.