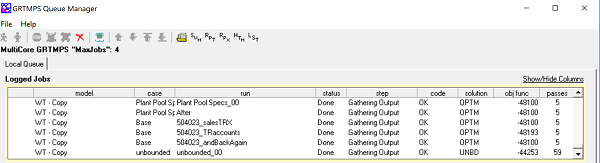
This is why the g5 input panel for utility purchases and sales gives you an error if you can buy electricity at 0.06 $/Kwh and sell it for 0.07.
This sort of checking however, isn’t done for the purchases and sales of streams, as those appear on different panels. The PGM has some code for detecting problems during matrix generation and there is also a matrix generation option to raise the purchase prices automatically, but, alas, on trying to make examples for this note, I found that they have fallen into disrepair – so that is something on my to-do list. In any case, it is not practical to make a complete pre-optimization check for unbounded structures, as in many cases it depends on indirect relationships between variables, and so would be very time consuming compared to letting the optimizer find it.
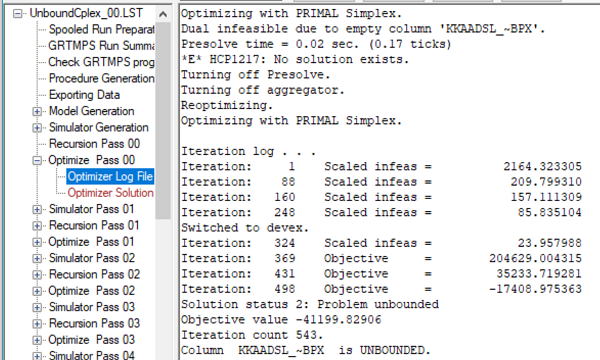
My unbounded example consists of a purchase at one location, transportation to another location, and a sale there. The purchase price plus the transportation costs are less than the sale price at the destination – and there are no limits on the amounts bought, transported or sold. The reports will tell us that the solution was unbounded, but don’t give any further details (another item for the to-do list). The optimizer solution (See #29 The Solution Print – It’s the Answer), however, will tell you which vector (column, variable) is causing the problem. The format of this depends on the optimizer.
HSLP marks the vector status as AT ++ in the solution prints in the LST / SPR files, like so:
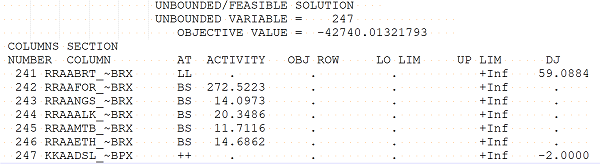
KKAADSL_~BPX is the purchase of diesel at location KK. (See #16 Decoding Matrix Row and Column Names). The annotated solution print file (.SPA) will help with understanding names, but does not provide as much information as the optimizer log about what is unbounded.
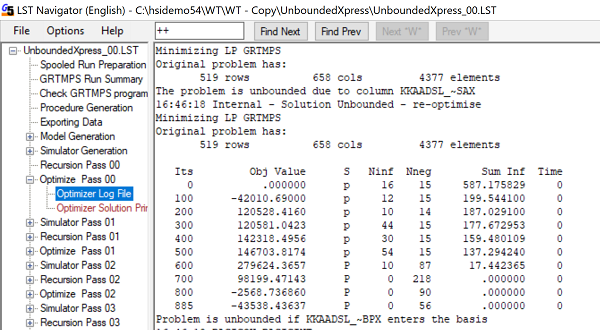
Our attention is also drawn to the sale vector, KKAADSL_~SAX.
Once you know what is unbounded, the solution is very simple. Add a constraint. The best way to do that depends on what the vector represents.
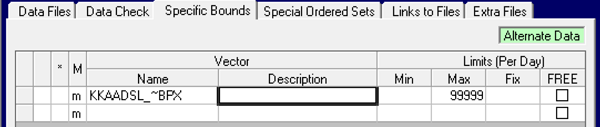
| For something like this, which is a purchase or sale, simply add a Max (TABLE 1BP.0). This should at least give you a feasible solution, so that you can track down any pricing mistakes or missing limits. Similarly if your unbounded vector represents an inventory or transportation option you can add a maximum where it was defined. |  |
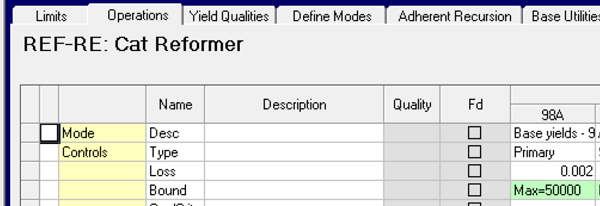 |
If your problem is a process unit (or recipe blend) operation, then a bound can be added on that mode, as here, which corresponds to TABLE 2(TN).4. If you are working in the database you need to remember that such unit changes apply to all cases where the unit is used, so if you are doing this for debugging it is a good idea to make a copy, either in the database or via the SSI, so you can get back to where you were. Although with a process unit it may also be more obvious that there should be an active limit. So, does your vector intersect with some loading rows? If not, which ones should be involved? If it does intersect, did you forget to constraint it? |
 |
 |
Once you have a feasible solution, you can inspect it for issues, such as faulty pricing or inconsistent operations. It is, of course, possible to have multiple causes of unbounded-ness in the same case. (Take off all the process maxima and all the P/S constraints!). As far as I can see, the optimizers only ever identify a single item; that is they stop as soon as they find the first problem. However, if you are running a recursed model, sometimes the item identified is not the same on every pass which might give you more information about the nature of the problem. If you add a constraint and the model remains unbounded, check to see if another vector has been identified and try again.
You want to reduce the risk of unbounded solutions? Then, as Vince deVita a very experienced modeller from Jacobs Consulting, says “Don’t let the model see infinity”. Even if you are running what is intended to be a very open case, you should be able to imagine some sky high upper limit on the purchases and / or sales that would not normally be constraining. (The optimizers, by the way, don’t like silly big values, so under 10E13.) You might even find that these help the optimization process even when you are not going unbounded. But don’t go crazy and limit absolutely every thing – or you just might go infeasible and make no money at all.
Comments and suggestions gratefully received via the usual e-mail addresses or here.
You may also use this form to ask to be added to the distribution list so that you are notified via e-mail when new articles are posted.